CS - 08 Numerical & Statistical Computing
Dec. 2001

1. (a) Which of the variable names given below are invalid in FORTRAN? Give reasons in support of your answer: (3)
(i) TEMP_X
(ii) ROLL2
(iii) PROGRAM

(b) Which are valid real constants in exponent form: (3)
(i) 0.01540E05
(ii) -0.148E - 5
(iii) 125.8E

(c) Write a FORTRAN statement for each of the following mathematical expressions: (3)
(i) ^{x1/3 - y-2}
(ii) a [(x + y)/z]^3.5
(iii) | sin X | + log 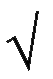(3X² + 5Y²)

(d) Suppose the variables A, B and C respectively contain the values 3, 4 and 5. Find the value of each of the following logical expressions: (3)
(i) (A + C) .EQ. 2 * B .AND. 2 * (C - A) .EQ. B
(ii) .NOT. (3 .EQ. C - 2 .AND. A .LE. C)
(iii) .NOT. C .GT. A .OR. B .LT. 5

(e) Write each of the following statements in FORTRAN: (3)
(i) If R = 2S + T, go to statement labelled 87
(ii) If S ¹ 11, go to statement labelled 44
(iii) If 3S > 4T, stop

(f) Draw a Pie Chart of the monthly expenses of a hostler, whose expenses per month are as follows: (3)

(g) Explain the concepts of 'skewness' and 'kurtosis' along with their significance in the study of distribution of mass of data. (4)

(h) A computer while calculating the correlation coefficient between 20 pairs of two variables x and y obtain the following results: (5)
n = 20, å x = 100, å y = 80, å x² = 520, å y² = 360, å xy = 420

It was later discovered at the time of checking that he had copied down two pairs as:

Obtain the correct value of correlation coefficient.

(i) Two dice are thrown. Find the probability that sum of the numbers on two dice is 9, given that first dice shows 6. (3)

2. (a) Write a FORTRAN 90 program that reads an n-digit number (for a positive integer n) and reverses the digits of the number to obtain a new number (e.g., if number 24379 is read then the new number obtained by reversing the digits is 97342). The program then prints the result with a suitable message. (8)

(b) Write a FORTRAN program that goes on reading values for an integer variable N until the value read is zero or negative. For each positive value of N read, the program tests whether N is a prime number or not. Also it should print appropriate messages. (7)

3. (a) Write a FORTRAN program that goes on reading sets of three real values until at least one of the values in any set of three values is zero or negative. The three values in a set denote lengths of the sides of a triangle. The program tests whether the triangle represented by the values is an equilateral triangle. If the triangle is equilateral then it computes the area of the triangle. If the triangle represented is not equilateral then it finds the perimeter of the triangle. Program prints suitable messages also. (7)

(b) Calculate the variance for the class-frequency distribution given below: (4)

(c) The income of 80 families are given below: (4)

4. (a) A five-figure number is obtained by the digits 0, 1, 2, 3, 4 (without repetition). Find the probability that the number formed is divisible by 4. (6)

(b) The average number of radioactive particles through a counter during 1 milli second in a laboratory experiment is 3. What is the probability that five particles enter the counter in a given millisecond? (4)

(c) The probability of a college student being male is 1/3 and that of being female is 2/3. The probability that a male student completes the course is 3/4 and that a female student does it is 1/2. A student is selected at random and is found to have completed the course. What is the probability that the student is a male? (5)

5. (a) Fit a straight line trend by the method of least squares to the following data: (7)

(b) The following table gives the average wholesale prices of the four grains for the years 1998 to 2001. Compute chain base index number. (8)

6. (a) Compute the approximate value of the integral
I =(1 + x + x²) dx
using Simpson's rule by taking interval size h as 1. (7)

(b) Find the value of cosh = d/dx (sinh x) at x = 1.52 from the following table: (8)

Previous Paper  Next Paper

UNIVERSAL TEACHER PUBLICATIONS
Web: www.universalteacherpublications.com, www.universalteacher.com