Sample Papers by Universal Teacher Publications

i) z = |x² - y²| + 6 e^x . y
ii) z =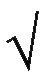

cos² (xy) + ((x)y)^z
iii) z = {ab/(c+d)}²

b) Which of the following variables names are invalid in FORTRAN 90? Why or why not?
i) THRI
ii) 50 + RATE
iii) END

c) Tell, which of the following FORTRAN constants are valid and why?
i) 12.5E + 4
ii) 85,79,823
iii) 3.6 E 7.3

d) Suppose the integer variables X and Y contain respectively 3 and 9. Find the final value of X and Y in each of the following cases:
i) IF (X.LE.Y) X = X +5
X = X + 3
ii) IF (X.EQ.Y + 2) GOTO 15
X = X + 3
15 X = X + Y

e) Suppose J, K, and L contain 10, 20, and 30 respectively. Find the value of each of the following logical expressions:
i) NOT (5.EQ.J-5 .AND.2*K.EQ.J+L)
ii) 2 * J .EQ. K. AND. K .LE. L

f) Draw a Pie chart of the monthly expenses of a hosteller, whose expense per month are as follows:

g) Explain the concepts of 'skewness' and kurtosis' along with their significance in the study distribution of mass of data.

h) A computer while calculating correlation coefficient between 20 pairs of two variables x and y obtains the following results:
n = 20, å x = 100, å y = 80, å x²= 520, å y²= 360, å xy = 420
It was later discovered at the time of checking that he had copied down two pairs as (6, 4) and (8, 6) of values of (x, y) instead of the correct values (8, 12) and (6, 8) respectively. Obtain the correct value of the correlation coefficient.

i) A jar contains five 50 paisa coins, four one rupee, three two rupee and four 5-rupee coins. A sample is taken out at random without replacement. Find the probability that the sample contains two 50-paisa coins, two one-rupee and one 5-rupee coins.

Q. 2. a) Write a FORTRAN function which reads a value x. If x ³ 1, then reads the value again. If 0 < x < 1
then computes f(x) = 1 + x²/2! + x⁴/4! + .... + x¹⁰⁰/100!
In order to terminate the function, value of x may be 0 or negative.

b) Write a program to convert any n-digit decimal number to equivalent hexadecimal number. For example hexadecimal equivalent to 43919 is AB8F.

where stock number is a 2 digit number. Item description is a 13 character name of the item and its quantity at hand is a 4 digit number, which is the number of items in hand/store. Unit price is the price of a single item. Develop a program to prepare sequential access file consisting of N records, each record refers to one item. The program should be such that it makes the following checks:
i) The stock number should not be outside 1 to 99.
ii) The initial data are to be entered from the terminal (unit =1)
iii) The price of an item should not be negative, and
iv) The number of terms of a particular type should not be negative.

b) For the following frequency distribution, draw (less-than type) frequency polygon:

Q. 4 a) A five figure number is formed by the digits 0,1,2,3,4 (without repetition). Find the probability that the number formed is divisible by 4.

b) The avarage number of radioactive particles through a counter during one millisecond in a laboratory experiment is 3. What is the probability that five particles enter the counter in a given millisecond?

c) The probability of a college student being male is 1/3 and that of being female is 2/3. The probability that a male student completes the course is 3/4 and that a female student does it is 1/2. A student is slelected at random and is found to have completed the course. What is the probability that the student is a male?

Q. 5. a) Calculate any one of the correlation coefficients for the following data:

The following table gives the average wholesome prices of four grains for the years 1996 to 2000. Compute the chain base index number:

I =

(1 + x² + x³) dx
using Trapezoidal rule or Simpson's rule by taking interval size h as 1.

x	y
1.0	2.7183
1.2	3.3201
1.4	4.0552
1.6	4.953
1.8	6.0496
2.0	7.3891
2.2	9.025

CS - 08 Numerical & Statistical Computing June 2003

CS - 08 Numerical & Statistical Computing
June 2003